1 The Monty Hall Problem

1.1 Diagramming the Solution

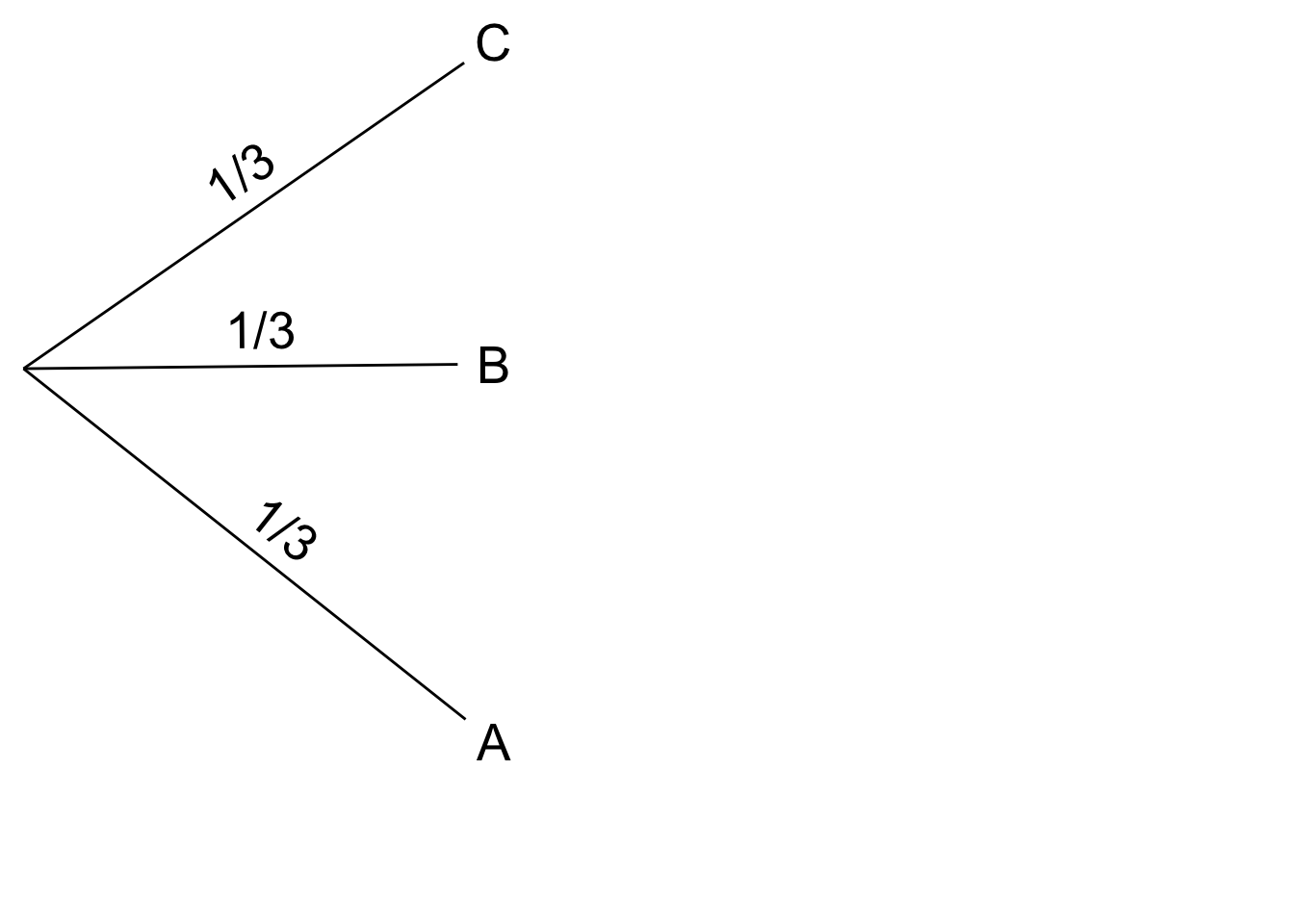Figure 1.2: First stage of a tree diagram for the Monty Hall problem

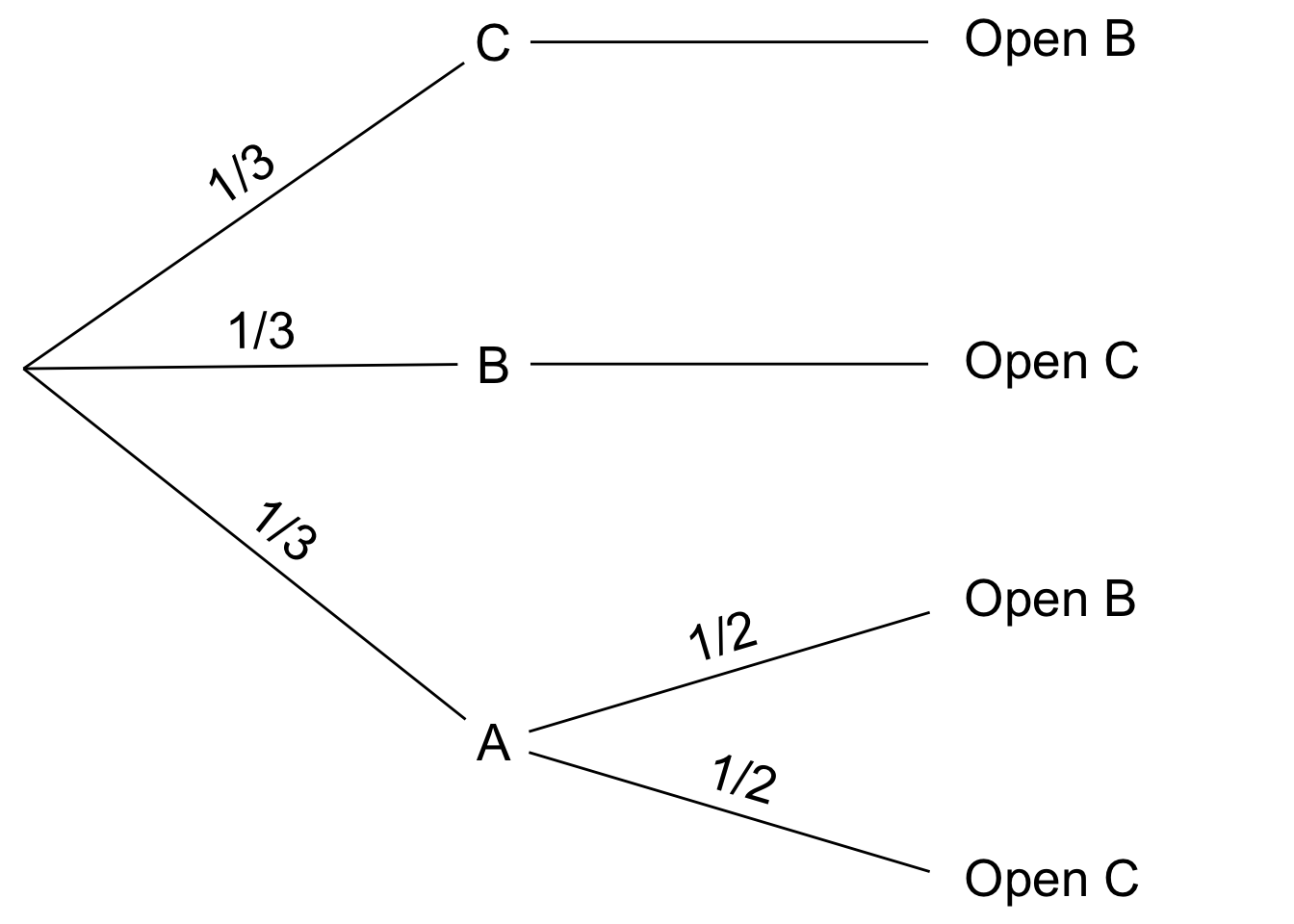Figure 1.3: Second stage

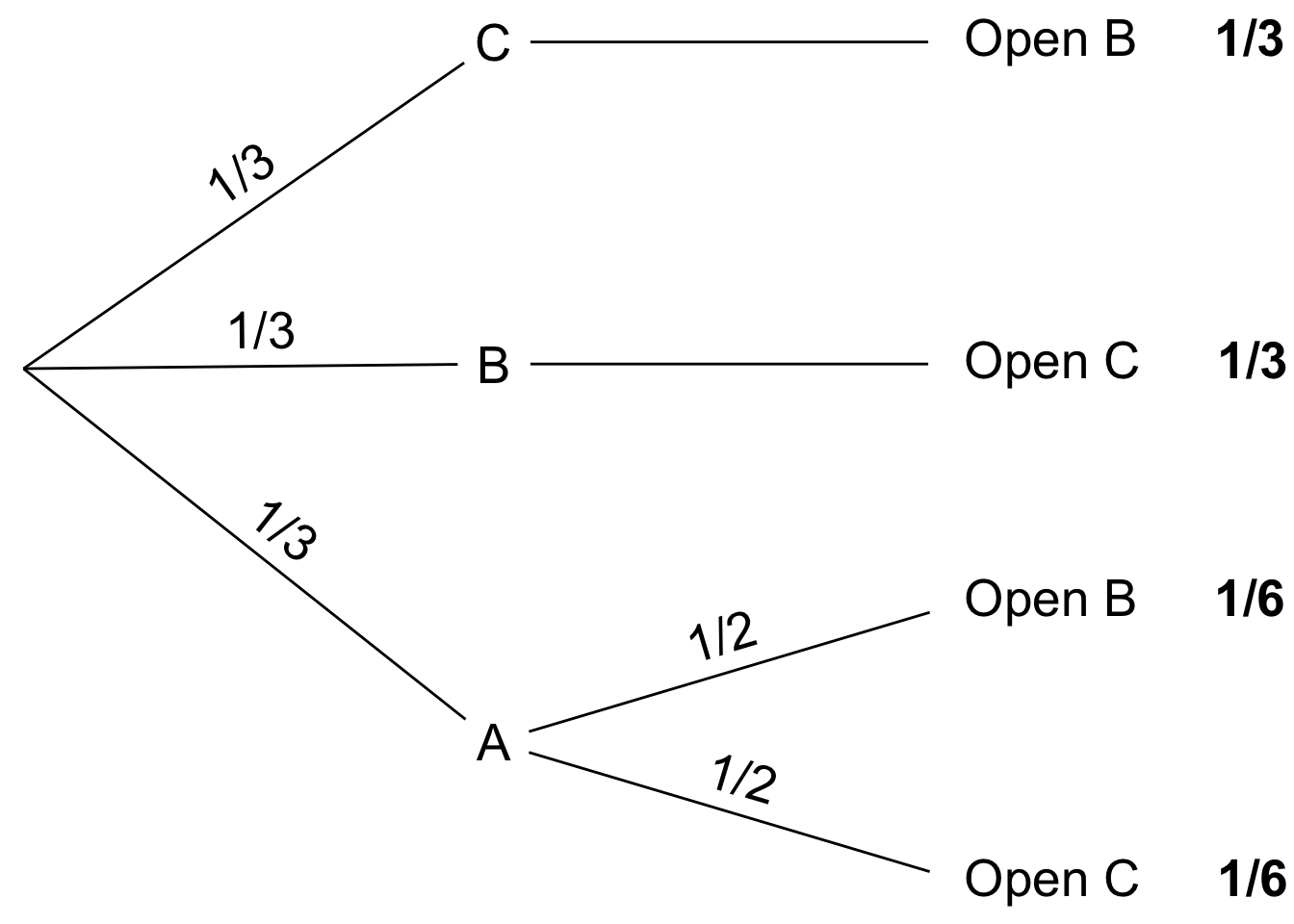Figure 1.4: Third and final stage

A picture helps clarify things. At first the prize could be behind any of the three doors, with equal probability each way. So we draw a tree with three branches, each labeled with a probability of \(1/3\). Figure 1.2 shows the result.

Now, which door the host opens may depend on where the prize is, i.e. which branch we’re on. If it’s behind door C, they won’t show you by opening that door. They would have to open door B in this case.

Likewise, if the prize is behind door B, then opening door C is their only option.

Only if the prize is behind door A do they have a choice: open either door B or door C. In that case it’s a tossup which door they’ll open, so each of those possibilities has a 1/2 chance. Check out Figure 1.3.

Now imagine playing the game over and over. A third of the time things will follow the top path; a third of the time they’ll follow the middle one; and the remaining third they’ll follow one of the two bottom paths.

When things follow the bottom branches, half of those times the host will open door B, and half the time they’ll open door C. So one in every six plays will follow the A-and-Open-B path. And one in every six plays will follow the A-and-Open-C path. See Figure 1.4.

Now we can understand what happens when the host opens door C. Usually it’s because the prize is behind door B. Sometimes they open door C because the prize is behind door A instead. But that’s only a sixth of the time, compared to a third of the time where they open door C because the prize is behind door B.

So when you see the host open door C, you should think it’s more likely you’re on the middle branch, with the prize behind door B. Switch!

1.2 Lessons Learned

Tree diagrams are a handy tool for solving probability problems. They also illustrate some central concepts of probability.

Probabilities are numbers assigned to possibilities. In the Monty Hall problem, there are three possibilities for where the prize is: door A, door B, and door C. Each of these possibilities starts with the same probability: 1/3.

Some possibilities are mutually exclusive, meaning only one of them can obtain. The prize can’t be behind door A and door B, for example. Here are more examples of mutually exclusive possibilities:

• A coin can land heads or tails, but it can’t do both on the same toss.
• A card drawn from a standard deck could be either an ace or a queen, but it can’t be both.
• The temperature at noon tomorrow could be 20 degrees, or it could be 25 degrees, but it can’t be both.

When possibilities are mutually exclusive, their probabilities add up. For example, the initial probability the prize will be behind either door A or door B is \(1/3 + 1/3 = 2/3\). And the probability a card drawn from a standard deck will be either an ace or a queen is \(4/52 + 4/52 = 8/52 = 2/13\).

Another key concept is possibilities that are exhaustive. In the Monty Hall problem, the prize has to be behind one of the three doors, so A, B, and C “exhaust” all the possibilities. Here are more examples of exhaustive possibilities:

• A card drawn from a standard deck must be either red or black.
• The temperature at noon tomorrow must be either above zero, below zero, or zero.

Figure 1.5: Three partitions for a card drawn from a standard deck

In our tree diagrams, each branch-point always uses a set of possibilities that is both exclusive and exhaustive. The first split on the three doors covers all the possibilities for where the prize might be, and only one of those possibilities can be the actual location of the prize. Likewise for the second stage of the diagram. On the bottom branch for example, the host must open either door B or door C given the rules, but he will only open one or the other.

When a set of possibilities is both exclusive and exhaustive, it’s called a partition. A partition “carves up” the space of possibilities into distinct, non-overlapping units.

There can be more than one way to partition the space of possibilities. For example, a randomly drawn playing card could be black or red; it could be a face card or not; and it could be any of the four suits (\(\heartsuit\), \(\diamondsuit\), \(\clubsuit\), \(\spadesuit\)).

When possibilities form a partition, their probabilities must add up to 1. Initially, the probability the prize will be behind one of the three doors is \(1/3 + 1/3 + 1/3 = 1\). And the probability that a card drawn from a standard deck at random will be either red or black is \(1/2 + 1/2 = 1\).

In a way, the fundamental principle of probability is that probabilities over a partition must add up to 1.

Tree diagrams follow a few simple rules based on these concepts. The parts of a tree are called nodes, branches, and leaves: see Figure 1.6.

Figure 1.6: The parts of a tree diagram: nodes, branches, and leaves

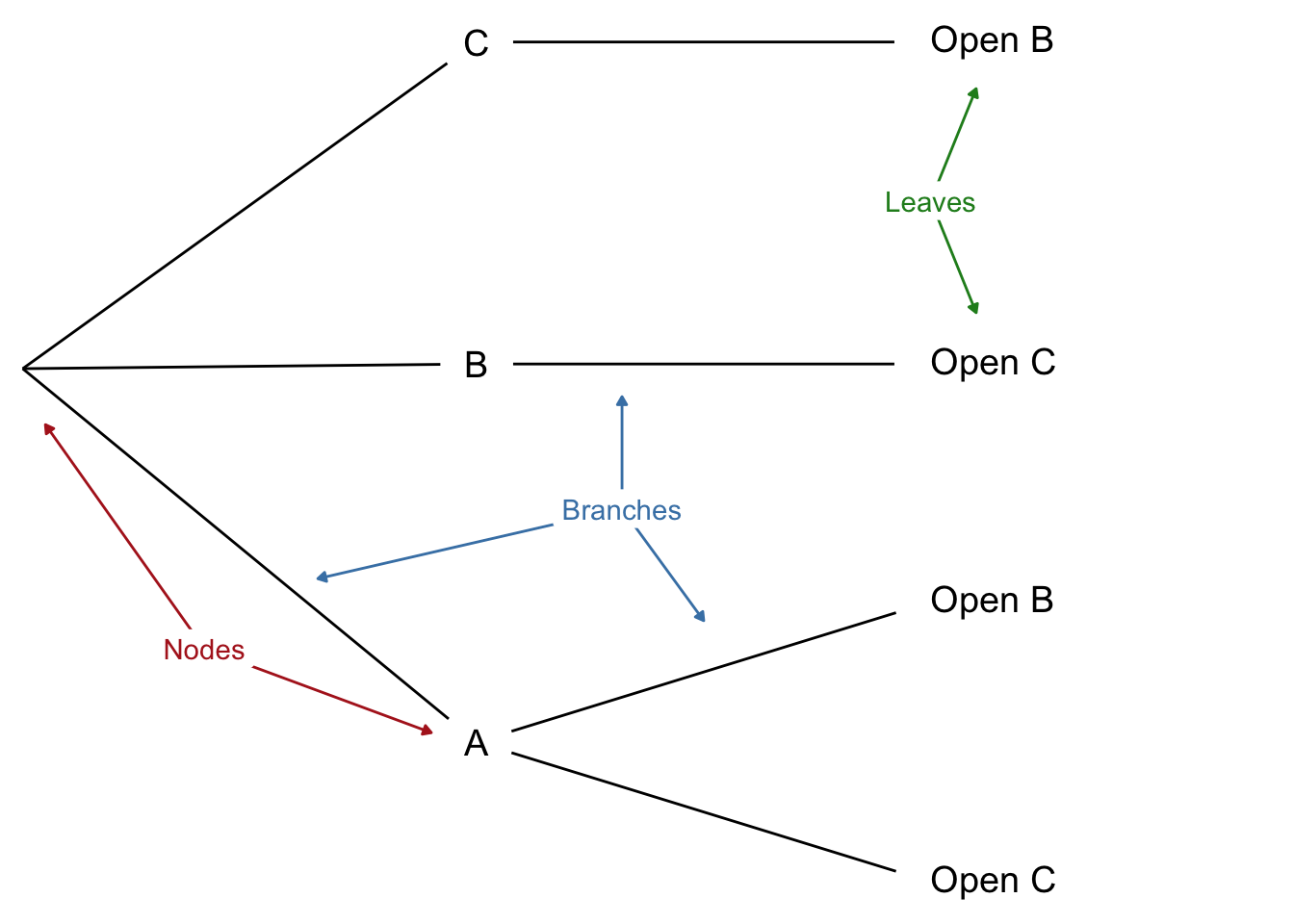
The rules for a tree are as follows.

• Rule 1. Each node must branch into a partition. The subpossibilities that emerge from a node must be mutually exclusive, and they must include every way the possibility from which they emerge could obtain.

• Rule 2. The probabilities emerging from a node must add to \(1\). If we add up the numbers on the branches immediately coming out of a node, they should add to \(1\).

• Rule 3. The probability on a branch is conditional on the branches leading up to it. Consider the bottom path in the Monty Hall problem. The probability the host will open door C is \(1/2\) there because we’re assuming the prize is behind door A.

• Rule 4. The probability of a leaf is calculated by multiplying across the branches on the path leading to it. This number represents the probability that all possibilities on that path occur.

Notice, Rule 4 is how we got the final probabilities we used to solve the Monty Hall problem (the numbers in bold).