This is the second in a trio of posts on simulated epistemic networks:
This post summarizes some key ideas from Rosenstock, Bruner, and O’Connor’s paper on the Zollman effect, and reproduces some of their results in Python. As always you can grab the code from GitHub.
Last time we met the Zollman effect: sharing experimental results in a scientific community can actually hurt its chances of arriving at the truth. Bad luck can generate misleading results, discouraging inquiry into superior options. By limiting the sharing of results, we can increase the chance that alternatives will be explored long enough for their superiority to emerge.
But is this effect likely to have a big impact on actual research communities? Or is it rare enough, or small enough, that we shouldn’t really worry about it?
Easy Like Sunday Morning
Last time we saw the Zollman effect can be substantial. The chance of success increased from .89 to .97 when 10 researchers went from full sharing to sharing with just two neighbours (from complete to cycle).
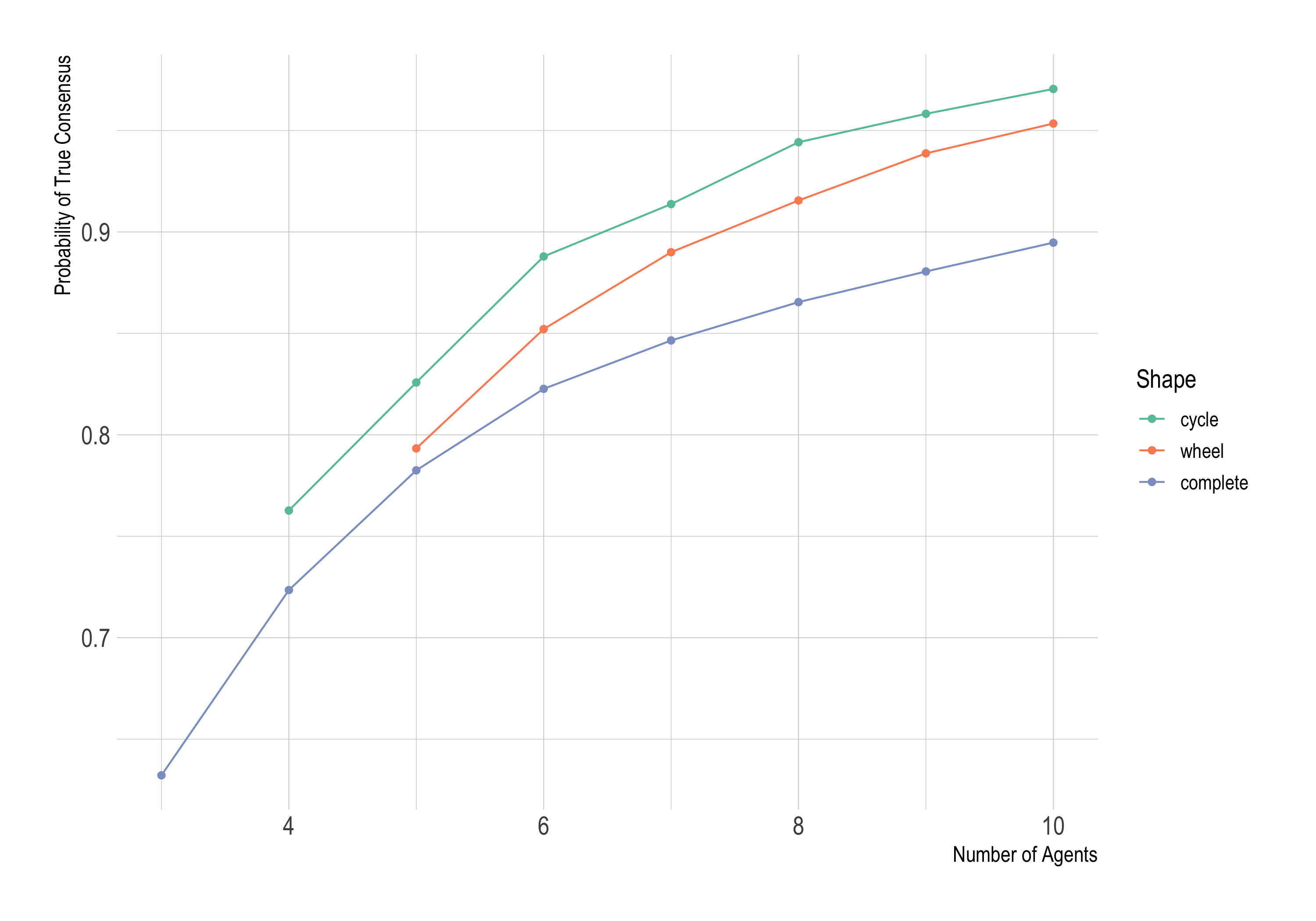
But that was assuming the novel alternative is only slightly better: .501 chance of success instead of .5, a difference of .001. We’d be less likely to get misleading results if the difference were .01, or .1. It should be easier to see the new treatment’s superiority in the data then.
So RBO (Rosenstock, Bruner, and O’Connor) rerun the simulations with different values for ϵ, the increase in probability of success afforded by the new treatment. Last time we held ϵ fixed at .001, now we’ll let it vary up to .1. We’ll only consider a complete network vs. a wheel this time, and we’ll hold the number of agents fixed at 10. The number of trials each round continues to be 1,000.
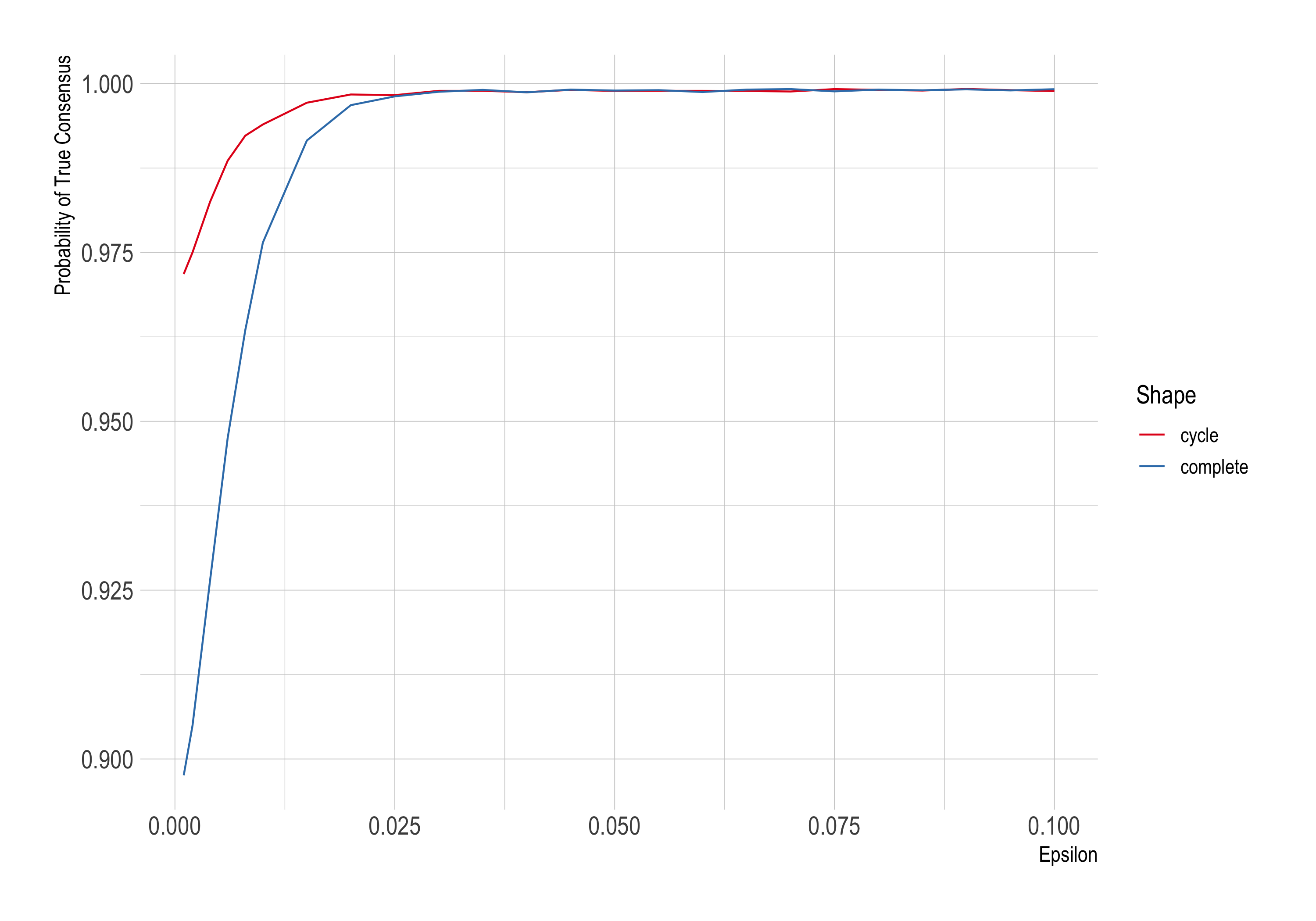
Here the Zollman effect shrinks as ϵ grows. In fact it’s only visible up to about .025 in our simulations.
More Trials, Fewer Tribulations
Something similar can happen as we increase n, the number of trials each researcher performs. Last time we held n fixed at 1,000, now let’s have it vary from 10 up to 10,000. We’ll stick to 10 agents again, although this time we’ll set ϵ to .01 instead of .001.
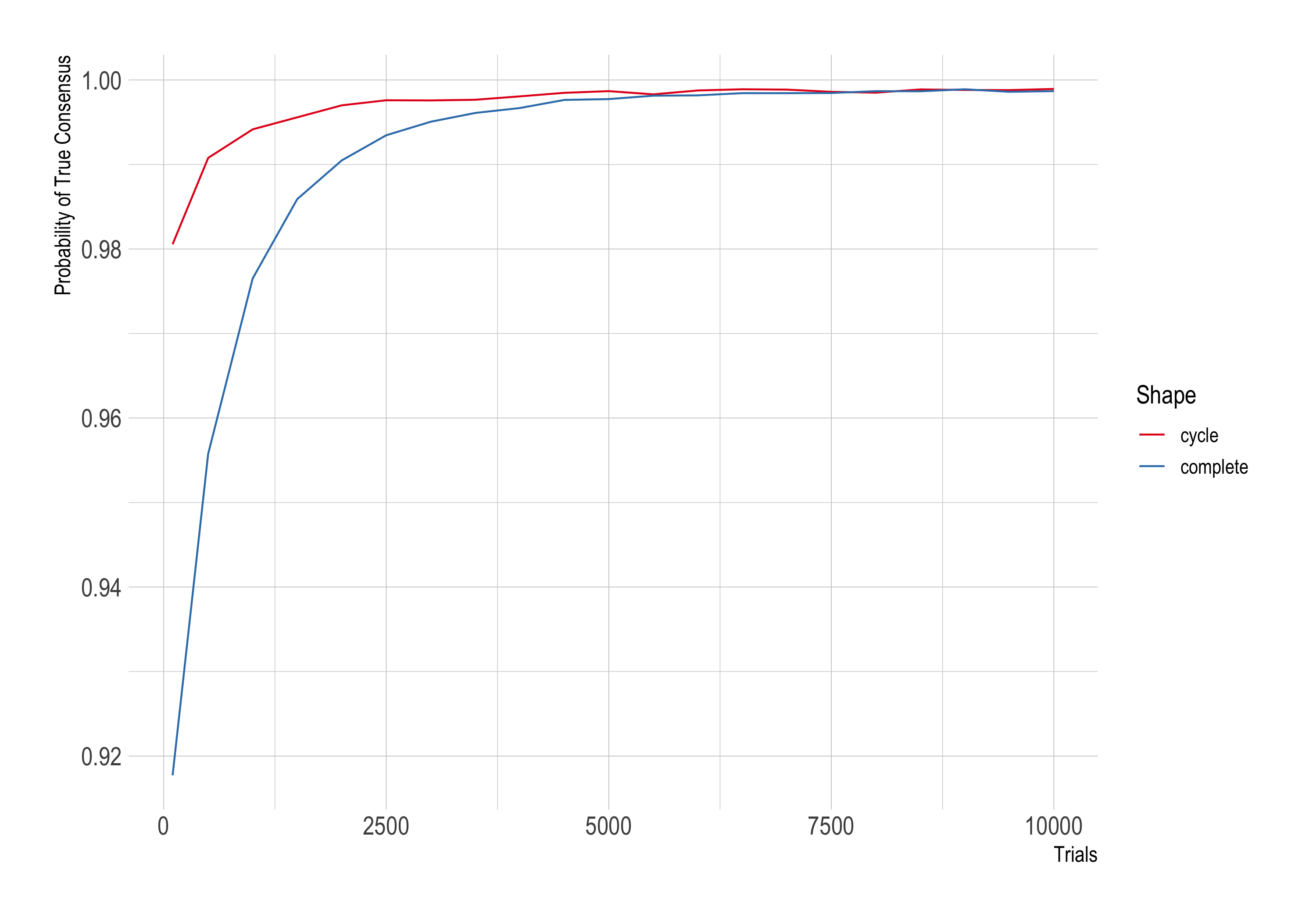
Again the Zollman effect fades, this time as the parameter n increases.
The emerging theme is that the easier the epistemic problem is, the smaller the Zollman effect. Before, we made the problem easier by making the novel treatment more effective. Now we’re making things easier by giving our agents more data. These are both ways of making the superiority of the novel treatment easier to see. The easier it is to discern two alternatives, the less our agents need to worry about inquiry being prematurely shut down by the misfortune of misleading data.
Agent Smith
Last time we saw that the Zollman effect seemed to grow as our network grew, from 3 up to 10 agents. But RBO note that the effect reverses after a while. Let’s return to n = 1,000 trials and ϵ = .001, so that we’re dealing with a hard problem again. And let’s see what happens as the number of agents grows from 3 up to 100.
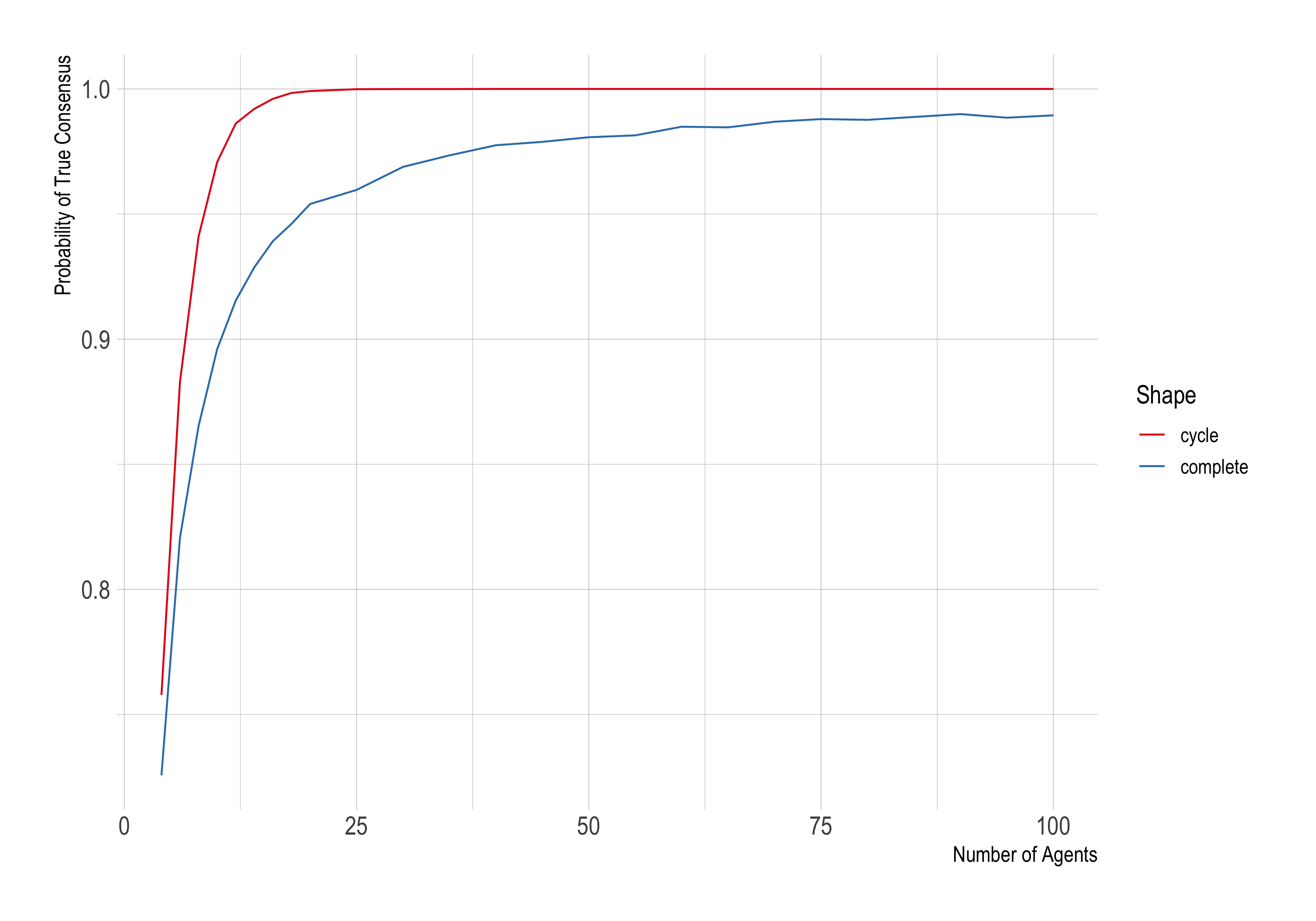
The effect grows from 3 agents up to around 10. But then it starts to shrink again, narrowing to a meagre .01 at 100 agents.
What’s happening here? As RBO explain, in the complete network a larger community effectively means a larger sample size at each round. Since the researchers pool their data, a community of 50 will update on the results of 25,000 trials at each round, assuming half the community has credence > 0.5. And a community of 100 people updates on the results of 50,000 trials, etc.
As the pooled sample size increases, so does the probability it will accurately reflect the novel treatment’s superiority. The chance of the community being misled drops away.
Conclusion
RBO conclude that the Zollman effect only afflicts epistemically “hard” problems, where it’s difficult to discern the superior alternative from the data. But that doesn’t mean it’s not an important effect. Its importance just depends on how common it is for interesting problems to be “hard.”
Do such problems crop up in actual scientific research, and if so how often? It’s difficult to say. As RBO note, the model we’ve been exploring is both artificially simple and highly idealized. So it’s unclear how often real-world problems, which tend to be messier and more complex, will follow similar patterns.
On the one hand, they argue, our confidence that the Zollman effect is important should be diminished by the fact that it’s not robust against variations in the parameters. Fragile effects are less likely to come through in messy, real-world systems. On the other hand, they point to some empirical studies where Zollman-like effects seem to crop up in the real world.
So it’s not clear. Maybe determining whether Zollman-hard problems are a real thing is itself a Zollman-hard problem?