This is post 3 of 3 on simulated epistemic networks (code here):
The first post introduced a simple model of collective inquiry. Agents experiment with a new treatment and share their data, then update on all data as if it were their own. But what if they mistrust one another?
It’s natural to have less than full faith in those whose opinions differ from your own. They seem to have gone astray somewhere, after all. And even if not, their views may have illicitly influenced their research.
So maybe our agents won’t take the data shared by others at face value. Maybe they’ll discount it, especially when the source’s viewpoint differs greatly from their own. O’Connor & Weatherall (O&W) explore this possibility, and find that it can lead to polarization.
Polarization
Until now, our communities always reached a consensus. Now though, some agents in the community may conclude the novel treatment is superior, while others abandon it, and even ignore the results of their peers using the new treatment.
In the example animated below, agents in blue have credence >.5 so they experiment with the new treatment, sharing the results with everyone. Agents in green have credence ≤.5 but are still persuadable. They still trust the blue agents enough to update on their results—though they discount these results more the greater their difference of opinion with the agent who generated them. Finally, red agents ignore results entirely. They’re so far from all the blue agents that they don’t trust them at all.
In this simulation, we reach a point where there are no more green agents, only unpersuadable skeptics in red and highly confident believers in blue. And the blues have become so confident, they’re unlikely to ever move close enough to any of the reds to get their ear. So we’ve reached a stable state of polarization.
How often does such polarization occur? It depends on the size of the community, and on the “rate of mistrust,” $m$. Details on this parameter are below, but it’s basically the rate at which difference of opinion increases discounting. The larger $m$ is, the more a given difference in our opinions will cause you to discount data I share with you.
Here’s how these two factors affect the probability of polarization. (Note: we’re considering only complete networks here.)
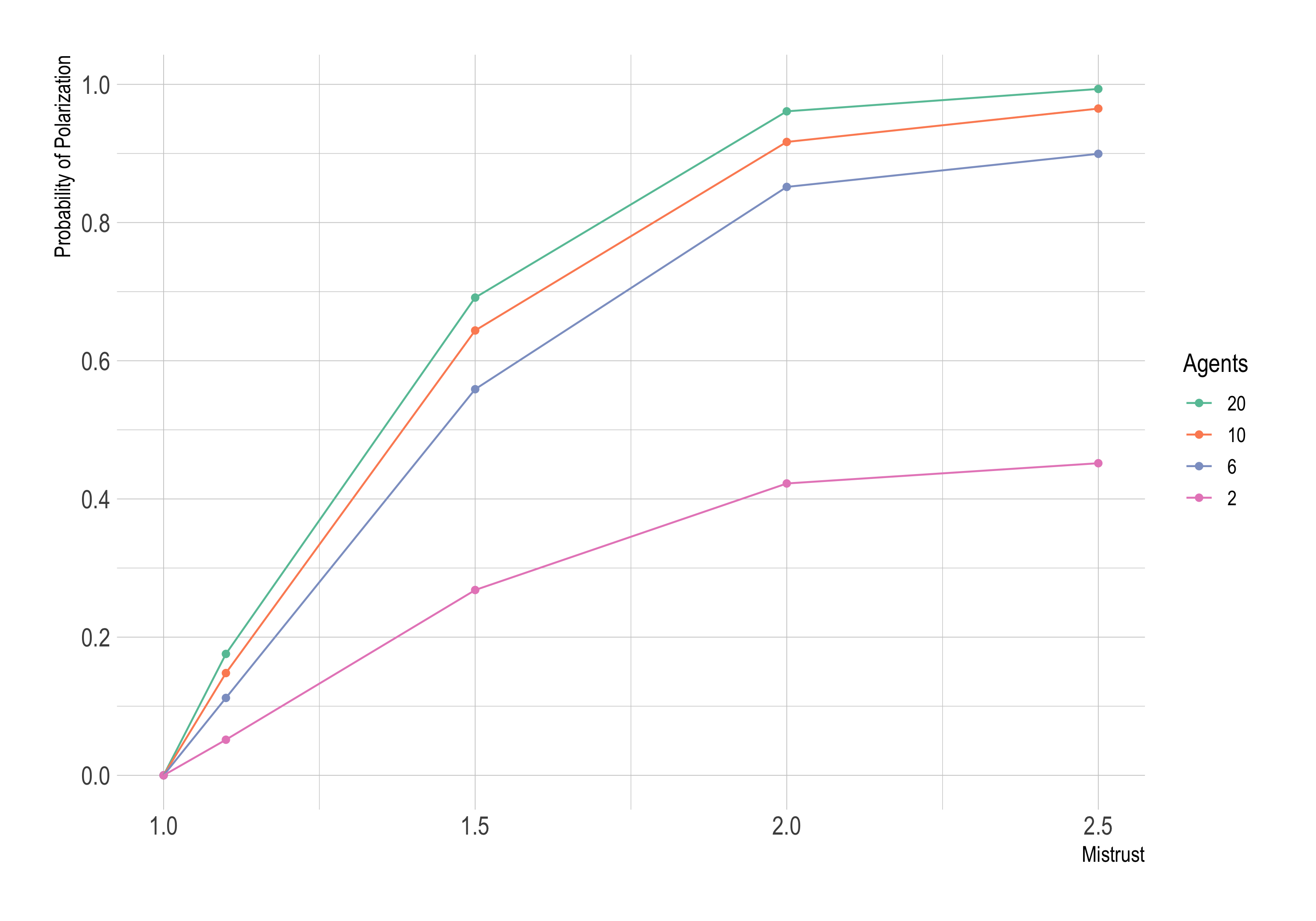
So the more agents are inclined to mistrust one another, the more likely they are to end up polarized. No surprise there. But larger communities are also more disposed to polarize. Why?
As O&W explain, the more agents there are, the more likely it is that strong skeptics will be present at the start of inquiry: agents with credence well below .5. These agents will tend to ignore the reports of the optimists experimenting with the new treatment. So they anchor a skeptical segment of the population.
The mistrust multiplier $m$ is essential for polarization to happen in this model. There’s no polarization unless $m > 1$. So let’s see the details of how $m$ works.
Jeffrey Updating
The more our agents differ in their beliefs, the less they’ll trust each other. When Dr. Nick reports evidence $E$ to Dr. Hibbert, Hibbert won’t simply conditionalize on $E$ to get his new credence $P’(H) = P(H \mathbin{\mid} E)$. Instead he’ll take a weighted average of $P(H \mathbin{\mid} E)$ and $P(H \mathbin{\mid} \neg E)$. In other words, he’ll use Jeffrey conditionalization: $$ P’(H) = P(H \mathbin{\mid} E) P’(E) + P(H \mathbin{\mid} \neg E) P’(\neg E). $$ But to apply this formula we need to know the value for $P’(E)$. We need to know how believable Hibbert finds $E$ when Nick reports it.
O&W note two factors that should affect $P’(E)$.
The more Nick’s opinion differs from Hibbert’s, the less Hibbert will trust him. So we want $P’(E)$ to decrease with the absolute difference between Hibbert’s credence in $H$ and Nick’s. Call this absolute difference $d$.
We also want $P’(E)$ to decrease with $P(\neg E)$. Nick’s report of $E$ has to work against Hibbert’s skepticism about $E$ to make $P’(E)$ high.
A natural proposal then is that $P’(E)$ should decrease with the product $d \cdot P(\neg E)$, which suggests $1 - d \cdot P(\neg E)$ as our formula. When $d = 1$ this would mean Hibbert ignores Nick’s report: $P’(E) = 1 - P(\neg E) = P(E)$. And when they are simpatico, $d = 0$, Hibbert will trust Nick fully and just conditionalizes on his report, since then $P’(E) = 1$.
This is fine from a formal point of view, but it means that Hibbert will basically never ignore Nick’s testimony completely. There is zero chance of $d = 1$ ever happening in our models.
So, to explore models where agents fully discount one another’s testimony, we introduce the mistrust multiplier, $m \geq 0$. This makes our final formula: $$P’(E) = 1 - \min(1, d \cdot m) \cdot P(\neg E).$$ The $\min$ is there to prevent negative values. When $d \cdot m > 1$, we just replace it with $1$ so that $P’(E) = P(E)$. Here’s what this function looks like for one example, where $m = 1.5$ and $P(E) = .6$:
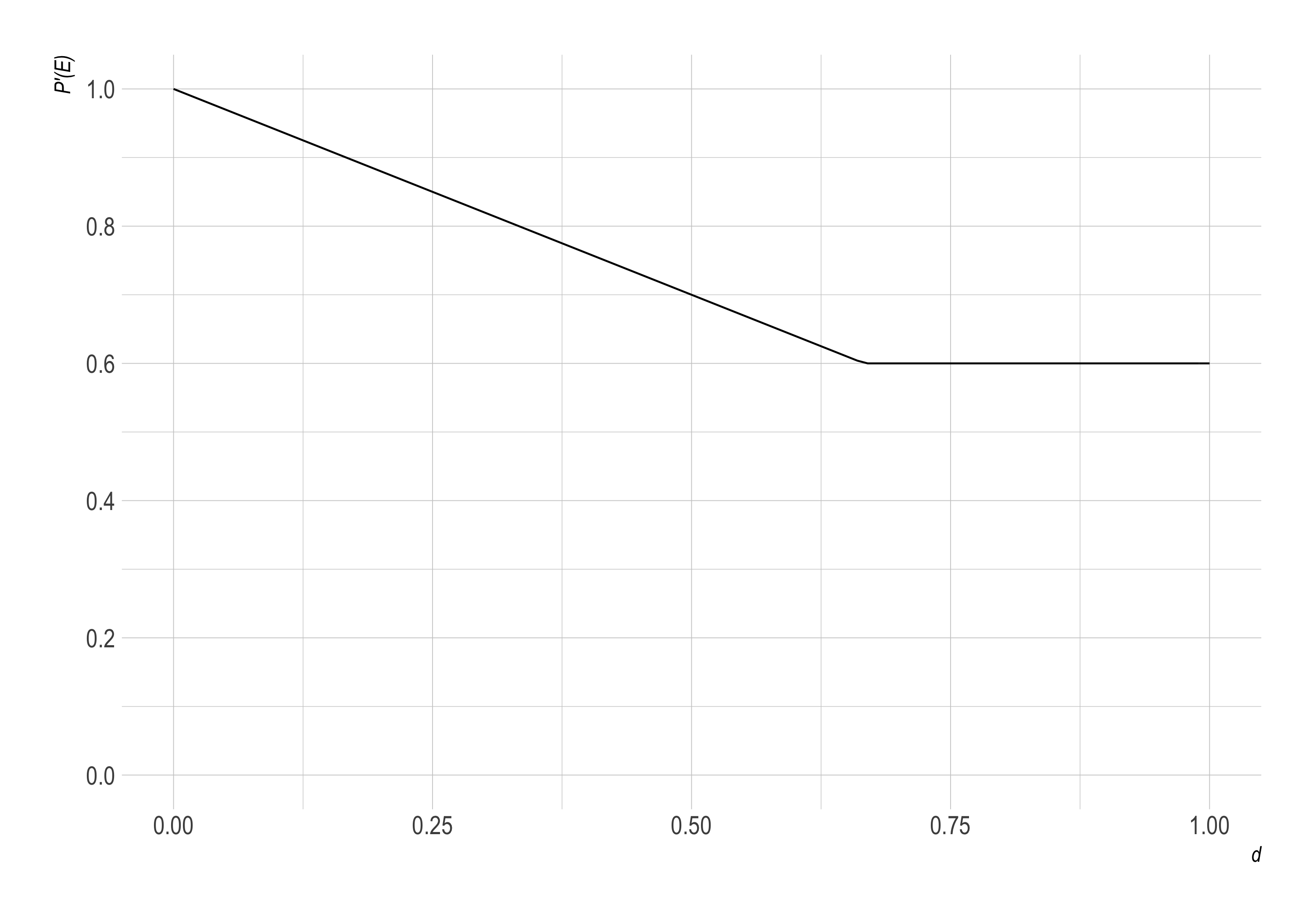
Note the kink, the point after which agents just ignore one another’s data.
O&W also consider models where the line doesn’t flatten, but keeps going down. In that case agents don’t ignore one another, but rather “anti-update.” They take a report of $E$ as a reason to decrease their credence in $E$. This too results in polarization, more frequently and with greater severity, in fact.
Discussion
Polarization only happens when $m > 1$. Only then do some agents mistrust their colleagues enough to fully discount their reports. If this never happened, they would eventually be drawn to the truth (however slowly) by the data coming from their more optimistic colleagues.
So is $m > 1$ a plausible assumption? I think it can be. People can be so unreliable that their reports aren’t believable at all. In some cases a report can even decrease the believability of the proposition reported. Some sources are known for their fabrications.
Ultimately it comes down to whether $P(E \,\vert\, R_E) > P(E)$, i.e. whether someone reporting $E$ increases the probability of $E$. Nothing in-principle stops this association from being present, absent, or reversed. It’s an empirical matter of what one knows about the source of the report.