Spare a thought for Reviewer 2, that much-maligned shade of academe. There’s even a hashtag dedicated to the joke:

A rare glimpse of reviewer 2, seen here in their natural habitat pic.twitter.com/lpT1BVhDCX

— Aidan McGlynn (@AidanMcGlynn) January 15, 2017

But is it just a joke? Order could easily matter here.

Referees invited later weren’t the editor’s first choice, after all. Maybe they’re less competent, less likely to appreciate your brilliant insights as an author. Or maybe they’re more likely to miss well-disguised flaws! Then we should expect Reviewer 2 to be the more generous one.

Come to think of it, we can order referees in other ways beside order-of-invite. We might order them according to who completes their report fastest, for example. And faster referees might be more careless, hence more dismissive. Or they might be less critical and thus more generous.

There’s a lot to consider. Let’s investigate, using Ergo’s data, as usual.

Severity & Generosity

Reviewer 2 is accused of a lot. It’s not just that their overall take is more severe; they also tend to miss the point. They’re irresponsible and superficial in their reading. And to the extent they do appreciate the author’s point, their objections are poorly thought out. What’s more, if they bother to demand revisions, their demands are unreasonable.

We can’t measure these things directly, of course. But we can estimate a referee’s generosity indirectly, using their recommendation to the editors as a proxy.

Ergo’s referees choose from four possible recommendations: Reject, Major Revisions, Minor Revisions, and Accept. To estimate a referee’s generosity, we’ll assign these recommendations numerical ranks, from 1 (Reject) up through 4 (Accept).

The higher this number, the more generous the referee; the lower, the more severe.

Invite Order

Is there any connection between the order in which referees are invited and their severity?

Usually an editor has to try a few people before they get two takers. So we can assign each potential referee an “invite rank”. The first person asked has rank 1, the second person asked has rank 2, and so on.

Is there a correlation between invite rank and severity?

Here’s a plot of invite rank (x-axis) and generosity (y-axis). (The points have non-integer heights because I’ve added some random “jitter” to make them all visible. Otherwise you’d just see an uninformative grid.)

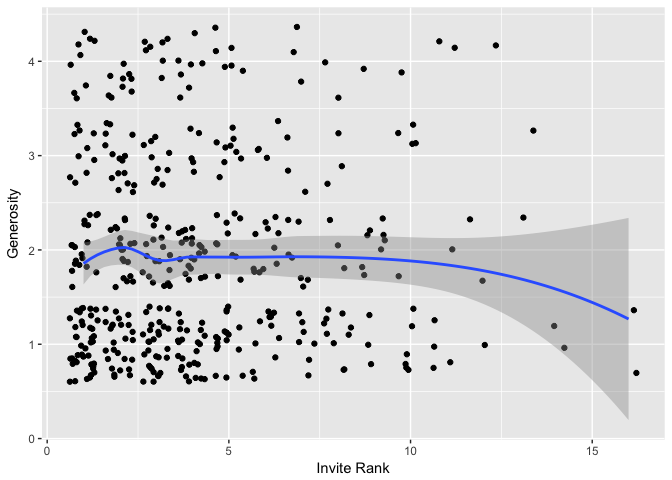
The blue curve shows the overall trend in the data.¹ It’s basically flat all the way through, except at the far-right end where the data is too sparse to be informative.

We can also look at the classic measure of correlation known as Spearman’s rho. The estimate is essentially 0 given our data ($r_s$ = 0.01).²

Evidently, invite-rank has no discernible impact on severity.

Speed

But now let’s look at the speed with which a referee completes their report:

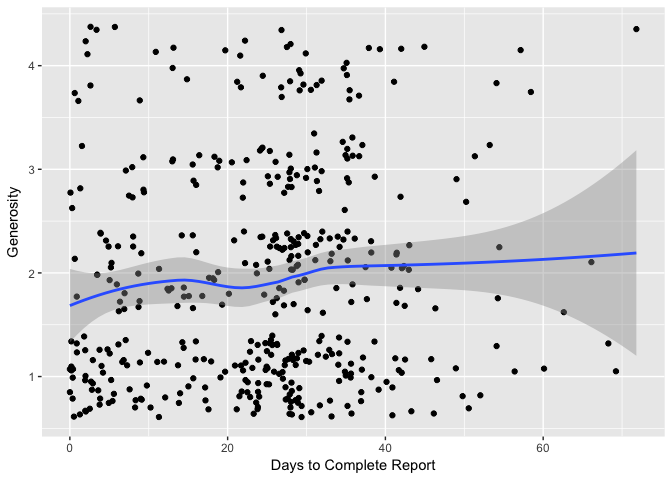
Here an upward trend is discernible. And our estimate of Spearman’s rho agrees: $r_s$ = 0.1, a small but non-trivial correlation.³

Apparently, referees who take longer tend to be more generous!

My Take

I find these results encouraging, for the most part.

It’s nice to know that an editor’s first choice for a referee is the same as their fifth, as far as how severe or generous they’re likely to be.

It’s also nice to know that the speed with which a referee completes their report doesn’t hugely inform heir severity.

One we might well worry that faster referees are unduly severe. But this worry is tempered by a few considerations.

For one thing, the effect we found is small enough that it could just be noise. It is detectable using tools like regression and significance testing, so it’s not to be dismissed out of hand. But we might also do well to heed the wisdom of XKCD here:

Even if the effect is real, though, it could be a good thing just as easily as a bad thing.

True, referees who work fast might be sloppy and dismissive. And those who take longer might feel guiltier and thus be unduly generous.

But maybe referees who are more on the ball are both more prompt and more apt to spot a submission’s flaws. Or (as my coeditor Franz Huber pointed out) manuscripts that should clearly be rejected might be easier to referee on average, hence faster.

It’s hard to know what to make of this effect, if it is an effect. Clearly, #MoreResearchIsNeeded.

Technical Notes

This post was written in R Markdown and the source is available on GitHub. I’m new to both R and statistics, and this post is a learning exercise for me. So I encourage you to check the code and contact me with corrections.