In the previous post we saw there’s about a $35$% chance a given referee will agree to review a paper for Ergo. And on average it takes about $5.8$ tries to find two referees for a submission. The full empirical distribution looks like this:

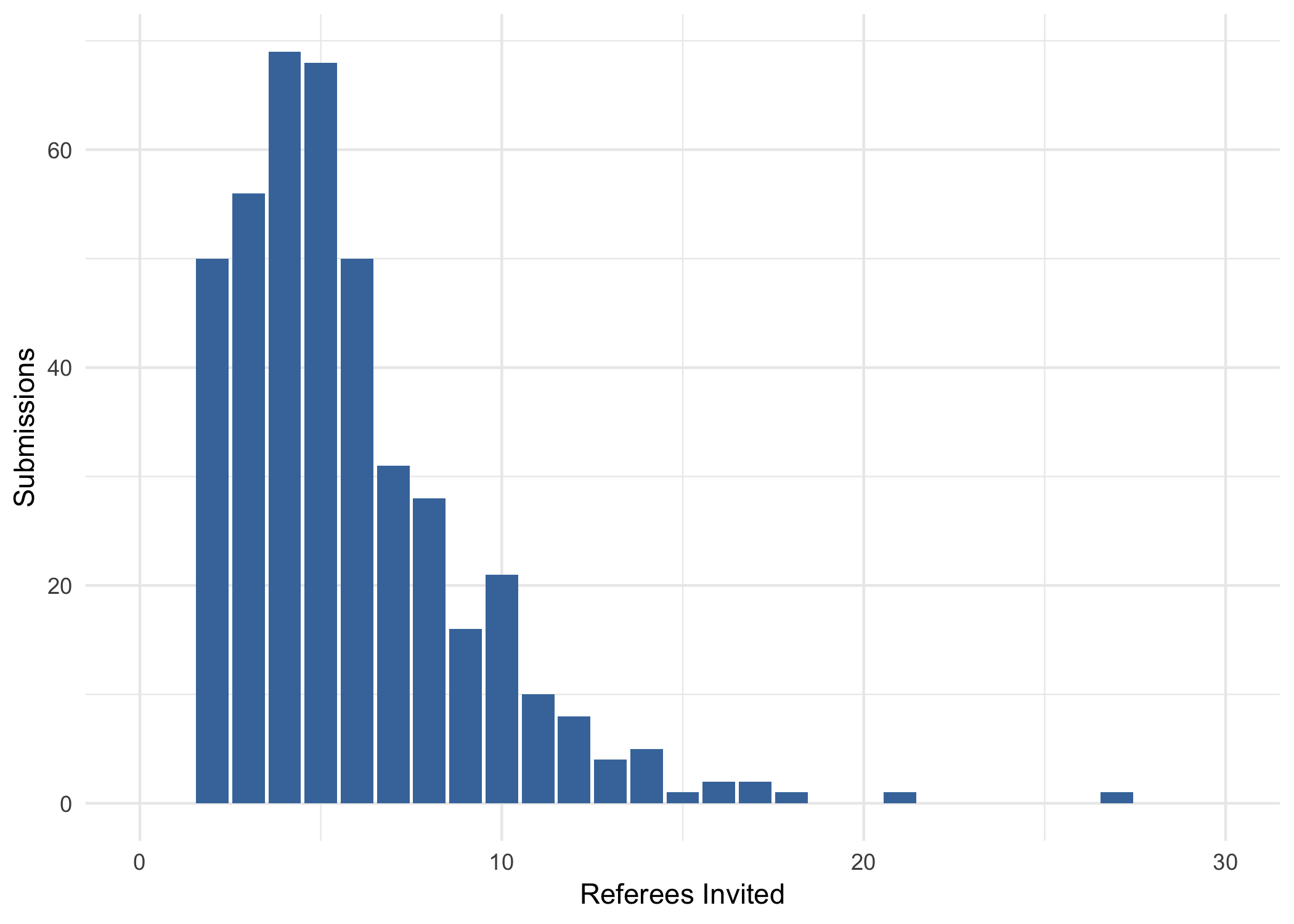
But there’s also an a priori way of exploring an editor’s predicament here, by using a classic model: the negative binomial distribution. So I thougth I’d make a little exercise of seeing how well the model captures the empirical reality here.

Contacting potential referees is a bit like flipping a loaded coin: you keep flipping until you get two heads, then stop. Our question is how many flips it’ll take to get to that point.

Let $p$ be the probability of heads on each toss, and let $T$ be the number of tails you get before landing the second head. The negative binomial model says the probability of getting $t$ tails, $P(T = t)$, is: $$ P(T = t) = \binom{t + 1}{t} p^t (1 - p)^2. $$ And the mean of this distribution is $2(1-p)/p$.

If the coin is fair, $p = .5$, and we should expect to get $T = 2$ tails: $$ 2(1-p)/p = 2(1-.5)/.5 = 2. $$ An editor’s “coin” is biased against them though, at least at Ergo: $p = .35$. So we would expect $T = 3.7$ referees on average to decline before we get two takers: $$ 2(1-p)/p = 2(1-.35)/.35 = 3.7. $$ In other words, we expect it to take on average $5.7$ tries to secure two referees for a submission, which very closely matches the empirical average of $5.8$!

How about the full distribution, how well does it match the empirical reality?

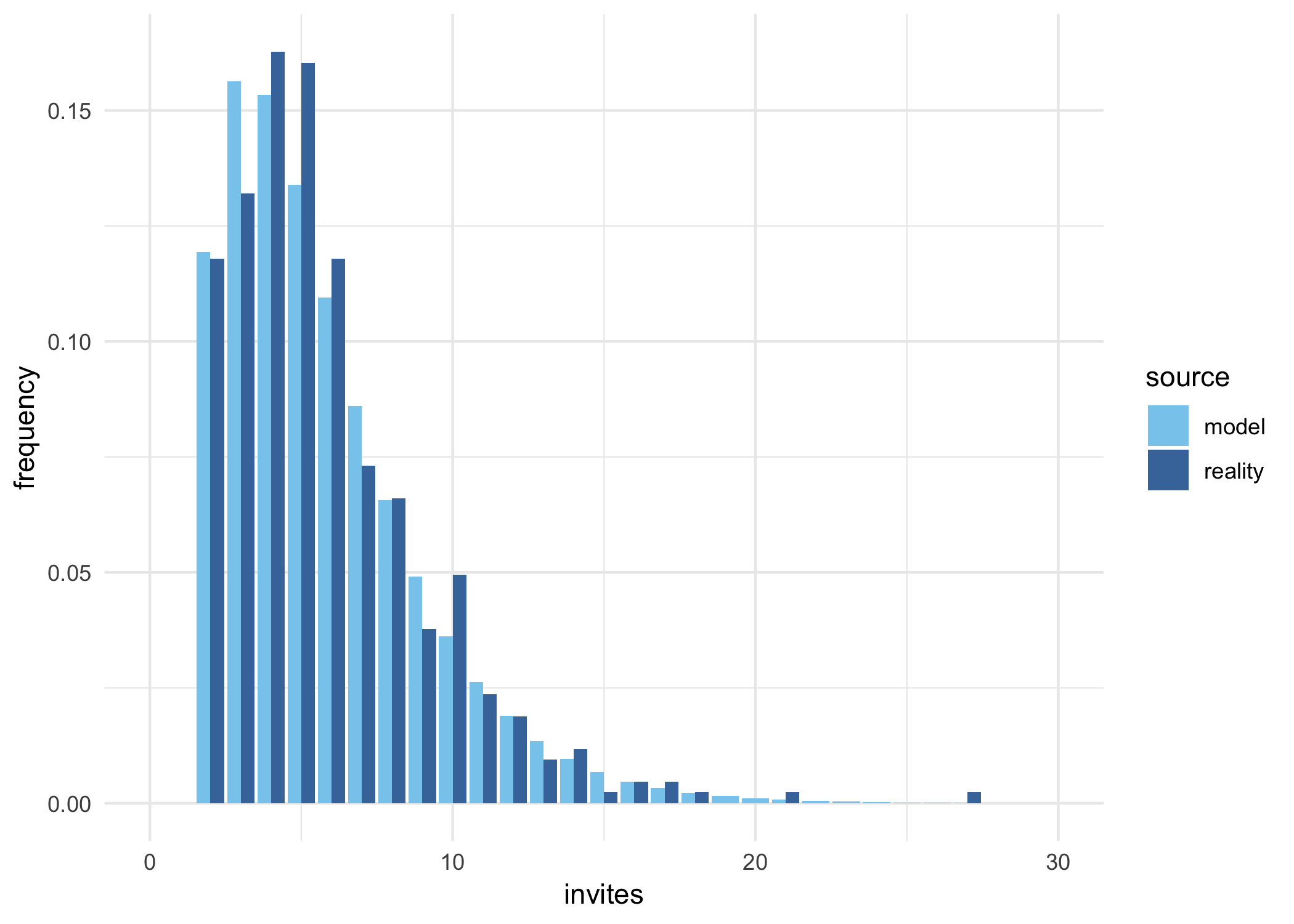
The model peaks a bit early, but otherwise it’s pretty accurate.

Of course, mileage may vary depending on the journal. For example, Ergo has a pretty high desk-rejection rate—about $67$%. And referees may be more willing to agree when they know a submission has already passed that hurdle.

So let’s conclude by looking at the model’s predictions when referees are more/less likely to agree. Here are the predictions for some plausible values of $p$. The mean $\mu$ is the corresponding number of invites required to secure two reviews, on average.

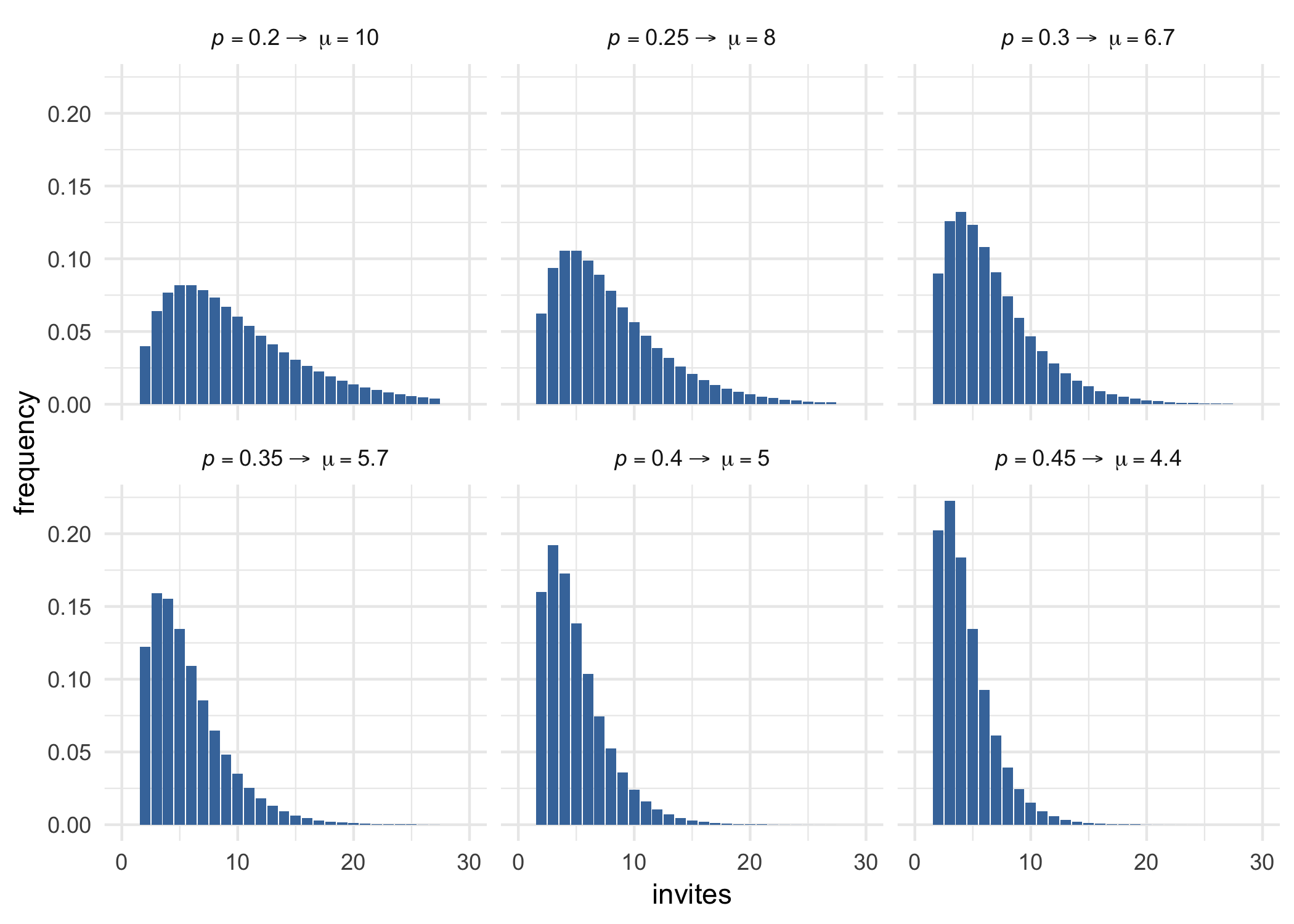
All these models assume that referees’ responses are independent, like flips of a coin, which isn’t too realistic. But given how close the model is for Ergo, it might still be good enough for other journals too.