Last time we saw that the set of probability assignments is convex. Today we’re going to show that convex sets have a special sort of “obtuse” relationship with outsiders. Given a point outside a convex set, there is always a point in the set that forms a right-or-obtuse angle with it.

Recall our 2D diagram from the first post. The convex set of interest here is the diagonal line segment from $(0,1)$ to $(1,0)$:

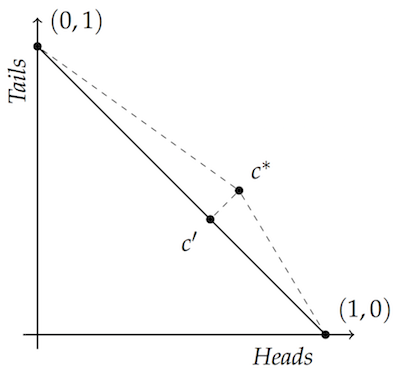
For any point outside the diagonal, like $c^* $, there is a point like $c’$ on it that forms a right angle with all other points on the diagonal. As a result, $c’$ is closer to all other points on the diagonal than $c^* $ is. In particular, $c’$ is closer to both vertices, so it’s always more accurate than $c^*$. It’s “closer to the truth”.

The insider point $c’$ that we used in this case is the closest point on the diagonal to $c^*$. That’s what licenses the right-triangle reasoning here. Today we’re generalizing this strategy to $n$ dimensions.

To do that, we need some tools for reasoning about $n$-dimensional geometry.$ \renewcommand{\vec}[1]{\mathbf{#1}} \newcommand{\x}{\vec{x}} \newcommand{\y}{\vec{y}} \newcommand{\z}{\vec{z}} \newcommand{\B}{B} $

Arithmetic with Arrows

You’re familiar with arithmetic in one dimension: adding, subtracting, and multiplying single numbers. What about points in $n$ dimensions?

We introduced two ideas for arithmetic with points last time. We’ll add a few more today, and also talk about what they mean geometrically.

Suppose you have two points $\x$ and $\y$ in $n$ dimensions: $$ \begin{align} \x &= (x_1, \ldots, x_n),\\
\y &= (y_1, \ldots, y_n). \end{align} $$ Their sum $\x + \y$, as we saw last time, is defined as follows: $$ \x + \y = (x_1 + y_1, \ldots, x_n + y_n). $$ In other words, points are added coordinate-wise.

This definition has a natural, geometric meaning we didn’t mention last time. Start by thinking of $\x$ and $\y$ as vectors—as arrows pointing from the origin to the points $\x$ and $\y$. Then $\x + \y$ just amounts to putting the two arrows end-to-point and taking the point at the end: 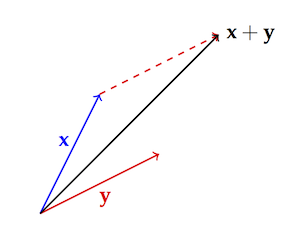(Notice that we’re continuing our usual practice of bold letters for points/vectors like $\x$ and $\y$, and italics for single numbers like $x_1$ and $y_3$.)

You can also multiply a vector $\x$ by a single number, $a$. The definition is once again coordinate-wise: $$ a \x = (a x_1, \ldots, a x_n). $$ And again there’s a natural, geometric meaning. We’ve lengthened the vector $\x$ by a factor of $a$. 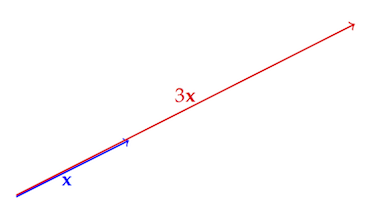Notice that if $a$ is between $0$ and $1$, then “lengthening” is actually shortening. For example, multiplying a vector by $a = 1/ 2$ makes it half as long.

If $a$ is negative, then multiplying by $a$ reverses the direction of the arrow. For example, multiplying the northeasterly arrow $(1,1)$ by $-1$ yields the southwesterly arrow pointing to $(-1,-1)$.

That means we can define subtraction in terms of addition and multiplication by negative one (just as with single numbers): $$ \begin{align} \x - \y &= \x + (-1 \times \y)\\
&= (x_1 - y_1, \ldots, x_n - y_n). \end{align} $$ So vector subtraction amounts to coordinate-wise subtraction.

But what about multiplying two vectors? That’s actually different from what you might expect! We don’t just multiply coordinate-wise. We do that and then add up the results: $$ \x \cdot \y = x_1 y_1 + \ldots + x_n y_n. $$ So the product of two vectors is not a vector, but a number. That number is called the dot product, $\x \cdot \y$.

Why are dot products defined this way? Why do we add up the results of coordinate-wise multiplication to get a single number? Because it yields a more useful extension of the concept of multiplication from single numbers to vectors. We’ll see part of that in a moment, in the geometric meaning of the dot product.

(There’s an algebraic side to the story too, having to do with the axioms that characterize the real numbers—the field axioms. We won’t go into that, but it comes out in this bit of a beautiful lecture by Francis Su, especially around the 11:45 mark.)

Signs and Their Significance

In two dimensions, a right angle has a special algebraic property: the dot-product of two arrows making the angle is always zero.

Imagine a right triangle at the origin, with one leg going up to the point $(0,1)$ and the other leg going out to $(1,0)$: 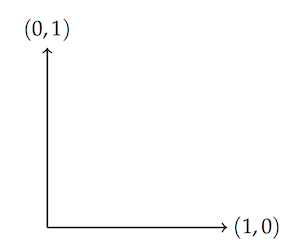The dot product of those two vectors is $(1,0) \cdot (0,1) = 1 \times 0 + 0 \times 1 = 0$. One more example: consider the right angle formed by the vectors $(-3,3)$ and $(1,1)$. 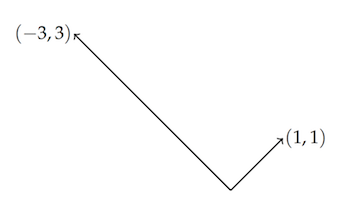Again, the dot product is $(-3,3) \cdot (1,1) = -3 \times 1 + 3 \times 1 = 0.$

Going a bit further: the dot product is always positive for acute angles, and negative for obtuse angles. Take the vectors $(5,0)$ and $(-1,1)$: Then we have $(5,0) \cdot (-1,1) = -5$. Whereas for $(5,0)$ and $(1,1)$: we find $(5,0) \cdot (1,1) = 5$.

So the sign of the dot-product reflects the angle formed by the vectors $\x$ and $\y$:

• acute angle: $\x \cdot \y > 0$,
• right angle: $\x \cdot \y = 0$,
• obtuse angle: $\x \cdot \y < 0$.

That’s going to be key in generalizing to $n$ dimensions, where reasoning with diagrams breaks down. But first, one last bit of groundwork.

Algebra with Arrows

You can check pretty easily that vector addition and multiplication behave a lot like ordinary addition and multiplication. The usual laws of commutativity, associativity, and distribution hold:

• $\x + \y = \y + \x$.
• $\x + (\y + \z) = (\x + \y) + \z$.
• $a ( \x + \y) = a\x + a\y$.
• $\x \cdot \y = \y \cdot \x$.
• $\x \cdot (\y + \z) = \x\y + \x\z$.
• $a (\x \cdot \y) = a \x \cdot \y = \x \cdot a \y$.

One notable consequence, which we’ll use below, is the analogue of the familiar “FOIL method” from high school algebra: $$ \begin{align} (\x - \y)^2 &= (\x - \y) \cdot (\x - \y)\\
&= \x^2 - 2 \x \cdot \y + \y^2. \end{align} $$ We’ll also make use of the fact that the Brier distance between $\x$ and $\y$ can be written $(\x - \y)^2$. Why?

Let’s write $\B(\x,\y)$ for the Brier distance between points $\x$ and $\y$. Recall the definition of Brier distance, which is just the square of Euclidean distance: $$ \B(\x,\y) = (x_1 - y_1)^2 + (x_2 - y_2)^2 + \ldots + (x_n - y_n)^2. $$ Now consider that, thanks to our definition of vector subtraction: $$ \x - \y = (x_1 - y_1, x_2 - y_2, \ldots, x_n - y_n). $$ And thanks to the definition of the dot product: $$ (\x - \y) \cdot (\x - \y) = (x_1 - y_1)^2 + (x_2 - y_2)^2 + \ldots (x_n - y_n)^2. $$ So $\B(\x, \y) = (\x - \y) \cdot (\x - \y)$, in other words: $$ \B(\x, \y) = (\x - y)^2. $$

A Cute Lemma

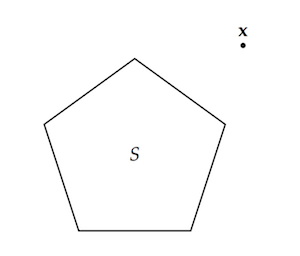
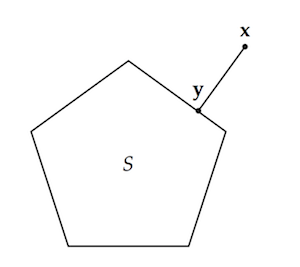
Now we can prove the lemma that’s the aim of this post. For the intuitive idea, picture a convex set $S$ in the plane, like a pentagon. Then choose an arbitrary point $\x$ outside that set: Now trace a straight line from $\x$ to the closest point of the convex region, $\y$: Finally, trace another straight line to any other point $\z$ of $S$: 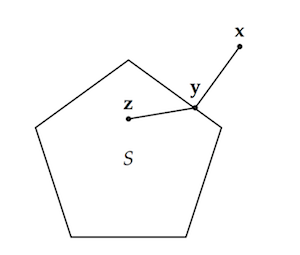No matter what point we choose for $\z$, the angle formed will either be right or obtuse. It cannot be acute.

Lemma. Let $S$ be a convex set of points in $\mathbb{R}^n$. Let $\x \not \in S$, and let $\y \in S$ minimize $\B(\y, \x)$ as a function of $\y$ on the domain $S$. Then for any $\z \in S$, $$ (\x - \y) \cdot (\z - \y) \leq 0. $$

Let’s pause to understand what the Lemma is saying before we dive into the proof.

Focus on the centered inequality. It’s about the vectors $\x - \y$ and $\z - \y$. These are the arrows pointing from $\y$ to $\x$, and from $\y$ to $\z$. So in terms of our original two dimensional diagram with the triangle: we’re looking at the angle between $c^*$, $c’$, and any point on the diagonal you like… which includes the ones we’re especially interested in, the vertices. What the lemma tells us is that this angle is always at least a right angle.

Of course, it’s exactly a right angle in this case, not an obtuse one. That’s because our convex region is just the diagonal line. But the Lemma could also be applied to the whole triangular region in the diagram. That’s a convex set too. And if we took a point inside the triangle as our third point, the angle formed would be obtuse. (This is actually important if you want to generalize the dominance theorem beyond what we’ll prove next time. But for us it’s just a mathematical extra.)

Now let’s prove the Lemma.

Proof. Because $S$ is convex and $\y$ and $\z$ are in $S$, any mixture of $\y$ and $\z$ must also be in $S$. That is, every point $\lambda \z + (1-\lambda) \y$ is in $S$, given $0 \leq \lambda \leq 1$.

Notice that we can rewrite $\lambda \z + (1-\lambda) \y$ as follows: $$ \lambda \z + (1-\lambda) \y = \y + \lambda(\z - \y). $$ We’ll use this fact momentarily.

Now, by hypothesis $\y$ is at least as close to $\x$ as any other point of $S$ is. So, in particular, $\y$ is at least as close to $\x$ as the mixtures of $\y$ and $\z$ are. Thus, for any given $\lambda \in [0,1]$: $$ \B(\y,\x) \leq \B(\lambda \z + (1-\lambda) \y, \x). $$ Using algebra, we can transform the right-hand side as follows: $$ \begin{align} \B(\lambda \z + (1-\lambda) \y, \x) &= \B(\x, \lambda \z + (1-\lambda) \y)\\
&= \B(\x, \y + \lambda(\z - \y))\\
&= (\x - (\y + \lambda(\z - \y)))^2\\
&= ((\x - \y) - \lambda(\z - \y))^2\\
&= (\x - \y)^2 + \lambda^2(\z - \y)^2 - 2\lambda(\x - \y) \cdot (\z - \y)\\
&= \B(\x,\y) + \lambda^2\B(\z,\y) - 2\lambda(\x - \y) \cdot (\z - \y). \end{align} $$ Combining this equation with the previous inequality, we have: $$ \B(\y,\x) \leq \B(\x,\y) + \lambda^2\B(\z,\y) - 2\lambda(\x - \y) \cdot (\z - \y). $$ And because $\B(\y, \x) = \B(\x, \y)$, this becomes:
$$ 0 \leq \lambda^2\B(\z,\y) - 2\lambda(\x - \y) \cdot (\z - \y). $$ If we then restrict our attention to $\lambda > 0$, we can divide and rearrange terms to get: $$ (\x - \y) \cdot (\z - \y) \leq \frac{\lambda\B(\z,\y)}{2}. $$ And since this inequality holds no matter how small $\lambda$ is, it follows that $$ (\x - \y) \cdot (\z - \y) \leq 0, $$ as desired. $\Box$

Taking Stock

Here’s what we’ve got from this post and the last one:

• Last time: the set of probability functions $P$ is convex.
• This time: given a point $\x$ outside $P$, there’s a point $\y$ inside $P$ that forms a right-or-obtuse angle with every other point $\z$ in $P$.

Intuitively, it should follow that:

• $\y$ is closer to every $\z$ in $P$ than $\x$ is.

And indeed, that’s what we’ll show in the next post!